ABC165
2日連続開催ABCの1日目.
結果
| 問題 | ACまでに要した時間 | AC | WA | TLE |
|---|---|---|---|---|
| A | 1:41 | 1 | 0 | 0 |
| B | 27:58 | 1 | 0 | 0 |
| C | : | 0 | 0 | 0 |
| D | 59:35 | 1 | 0 | 1 |
| Rating | 順位 |
|---|---|
| 637 (+28) | 4141 |
解答
C(解説AC)
解けなかった.
考えていたこと
- すべての式を連立方程式とみなしても答えは一意に決まる訳じゃなさそうだしどうするか.
- 仮にそうだとしてもどう表現してどう実装すればいいか分からん.
- 仮に全列挙する場合,無条件で並べれば1010だし全探索は間に合いそうにない(これは勘違い.広義単調増加数列なので最大の空間計算量は
).
- わからん.ダメだ.次いこ.
すぬけさんの解説放送観ながら解いたやつ.vector<T>.back() をうまく使うと最小桁以上の値のみを次にpushできるため結果的に広義単調増加数列になる.頭良すぎてワラタ.これを応用すると(広義)単調減少数列も作れる.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; vector<int> a, b, c, d; int N, M, Q; int ans; void dfs(vector<int> A, int size) { if (size == N) { int now = 0; REP(i, Q) { if (A.at(b.at(i)) - A.at(a.at(i)) == c.at(i)) { now += d.at(i); } } ans = max(ans, now); return; } A.push_back(A.back()); while (A.back() <= M) { dfs(A, size + 1); ++A.back(); } } int main() { cin.tie(0); ios::sync_with_stdio(false); cin >> N >> M >> Q; a = b = c = d = vector<int>(Q); REP(i, Q) { cin >> a.at(i) >> b.at(i) >> c.at(i) >> d.at(i); --a.at(i); --b.at(i); } ans = 0; dfs(vector<int>(1, 1), 1); cout << ans << endl; return 0; }
D
解析的に解けなさそうと思い,適当にxを大きくして数式の結果をprintしたら周期性が見えたのと,何となく数式からも周期性が垣間見えるのでそれで出したらAC
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); long double A, B, N; cin >> A >> B >> N; long double a_b = A / B; long double x = min(N, B - 1); cout << floor(a_b * x) - A * floor(x / B) << endl; return 0; }
考えていたこと
- もうダメだ
- とりあえずどういう動きするか分からないので
をxごとにprintしてxに対してどう反応するか見てみるか
- お,周期性あるやん.しかも最大値は一定
- 言われてみれば
は単調増加していくけど
はxの値に関係なくB-1以上にはならないので周期性が生じるのも分かる気がする.
- じゃあ
で与題は最大になるのか?
- やってみるか.通った.マジか.
E(解説AC)
コンテスト中は全く解法が思いつかなかった問題.しかし適当にNとMを設定してみるとどういう時にダメになるかは明確.
イメージとしては,以下のように問題を噛み砕くと解法が分かる.
- N人のメンバーを
]の数列の上に並べ,その数列上で各メンバーを右に一個ずつスライドさせる操作をN回行う.その間に,対戦卓に書かれた番号(
とする)と,その時点でメンバーがいる数値と一致した時に同じ相手と2回以上当たったらNG.
- 対戦卓に入ったときに同じやつと2回以上当たる条件は,対戦卓の番号の差が同じ時.∵各メンバーの数値は固定で1だけ単調増加するため差は変化しない.
- 一方で,N+1の番号になったメンバーは1に戻るため,Nが偶数の場合は
と
が一致する場合も上記の理由で2回当たってしまうためNGとなる.奇数の場合はこのケースは発生しない*1.
- 以上の考察により,
]において左端(1)と右端(N)から順番に舐めていき,
かつ一度も見たことがないパターンを列挙していけばよい.そのようなパターンに遭遇したら左端か右端をどちらか一個進めることで回避できる.
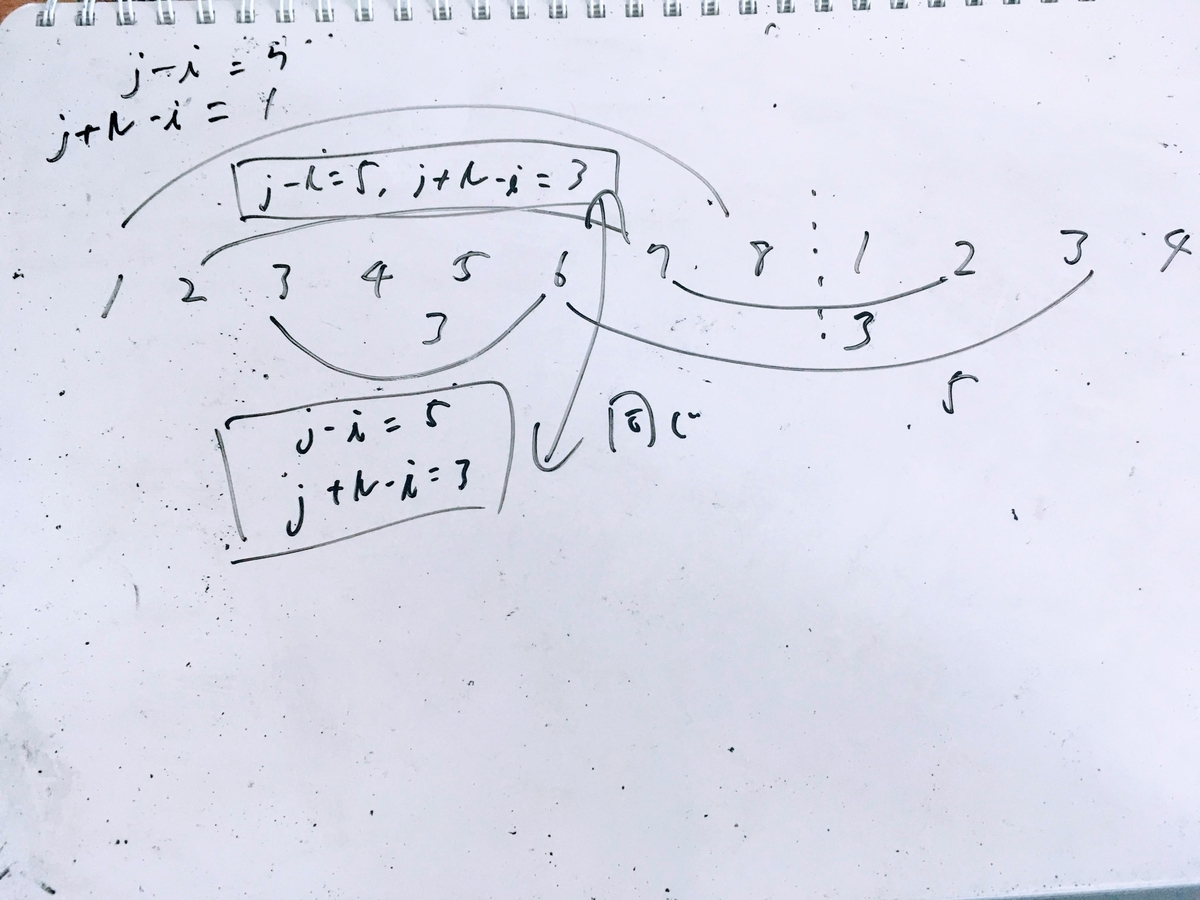
と
の関係
自分の考察は上記のリストのうち2番目にすら至らなかった.できなかった理由として,他の解答者がやっているような「最小のNとMのケースで考える」を試さなかった為であると考えられる.
似たようなパターンで「直線上に並んだN個の家の任意の家から別の任意の家へ移動するときの最短距離を求めよ」みたいな問題を見たことがある.これはで解けたが,循環数列(と見なせるもの)に対する操作を可能にする条件を求める問題も典型問題のうちのようだ.今後は解けるようになっておく必要がある.でもこの問題は青パフォ問題みたいだしやっぱ難しい部類だったとは思う.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N, M; cin >> N >> M; int l = 1; int r = N; if (N % 2 == 1) { REP(i, M) { cout << l << " " << r << endl; ++l; --r; } } else { set<pair<int, int>> found; REP(i, M) { cout << l << " " << r << endl; ++l; --r; if (abs(r - l) == abs(l + N - r) || found.find(make_pair(min(abs(r - l), abs(l + N - r)), max(abs(r - l), abs(l + N - r)))) != found.end()) { ++l; } found.insert(make_pair(min(abs(r - l), abs(l + N - r)), max(abs(r - l), abs(l + N - r)))); } } return 0; }
追記
ABC165の解説放送を観るとすぬけさんがとても分かりやすい解説をしていた.
多角形としてN人のメンバーを並べると,対戦卓の組合わせをそれぞれの角をつなぐ線分として表現できる.この図を使うとどういうケースでOKになるか直感的に理解できる.

ここから学べる点としては,今回のような循環する数列を扱う場合には図で考えるのも一つの手段である.
ダメだった点
- Cの計算量を正確に見積もれなかった.単調増加数列なんだから全パターン拾っても
で済むというのは思いついてくれ.
- Bで一瞬怯んでしまったので飛ばして後でやろうとしたら他も難しかった->結果的にBのsubmitが遅くなって結果に影響したというパターンをまたやってしまったのでよくない.Bは瞬殺できるものとして絶対後回しにしない.
- Dはたまたま解けたけどあんまり再現性ないな.floor関数は
のようにモジュロ演算に置き換えて整数の世界だけで計算できることがわかったので,次回以降は解析的に解きたい.
- あとモジュロ演算の特性ももう一度計算しておく必要がある.Dはモジュロ演算の分配則を知らないと解析的には解けない.
良かった点
- Cが解けず,DのACも遅かったのでレートが下がるんじゃないかとヒヤヒヤしたがプラスになって良かった.B速解きができればもう少しレート挙げられただろうが.
おわりに
- パフォーマンスの分布を見ると,800以下のレートだとABC速解きが依然として高パフォーマンスを得る効果的な方法のように見える.
- しかし,今後緑,水色と上がっていった時にそれでは通用しなくなるのは傾向から明らかなので解けない問題をへらす努力も継続して必要.
- 全探索が実装できなかった点は大いに反省し,単調増加,単調減少,条件なしの3パターン数列の全列挙はできるようになっておく必要がある.
*1:色んな人の解説を読んだがこれを明確に説明しているものはなかった.謎