ABC218
1年3ヶ月ぶりにABCに出たのでブログを書くことにする.
結果
| 問題 | ACまでに要した時間 | AC | WA | TLE |
|---|---|---|---|---|
| A | 2:23 | 1 | 0 | 0 |
| B | 2:29 | 1 | 0 | 0 |
| C | : | 0 | 1 | 0 |
| D | : | 0 | 0 | 0 |
| E | : | 0 | 0 | 0 |
| F | : | 0 | 0 | 0 |
| 新Rating | Performance | 順位 |
|---|---|---|
| 627 (-9) | 553 | 4622 |
解答
C
の解法しか思いつかず,そのままsubmitして見事TLEとWAも踏んだ.WAになったのは恐らく平行移動の探索範囲が甘いか何かだと思われる.
ダメ実装
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N; cin >> N; vector<vector<char>> S(N, vector<char>(N)); vector<vector<char>> S90(N, vector<char>(N)); vector<vector<char>> S180(N, vector<char>(N)); vector<vector<char>> S270(N, vector<char>(N)); int s_count = 0; REP(i, N) { REP(j, N) { cin >> S.at(i).at(j); S90.at(j).at(N - 1 - i) = S.at(i).at(j); S180.at(N - 1 - i).at(N - 1 - j) = S.at(i).at(j); S270.at(N - 1 - j).at(i) = S.at(i).at(j); if (S.at(i).at(j) == '#') { ++s_count; } } } vector<vector<char>> T(N, vector<char>(N)); int t_count = 0; REP(i, N) { REP(j, N) { cin >> T.at(i).at(j); if (T.at(i).at(j) == '#') { ++t_count; } } } if (s_count != t_count) { cout << "No" << endl; return 0; } REP(i, N * 2 - 2) { REP(j, N * 2 - 2) { int match_count = 0; REP(k, i + 1) { REP(l, j + 1) { if ((0 <= (N - 1 - k) && (N - 1 - k) <= N - 1) && (0 <= (N - 1 - l) && (N - 1 - l) <= N - 1) && (0 <= (i - k) && (i - k) <= N - 1) && (0 <= (j - l) && (j - l) <= N - 1)) { if (S.at(N - 1 - k).at(N - 1 - l) == '#' && T.at(i - k).at(j - l) == '#') { ++match_count; } } } } if (s_count == match_count) { cout << "Yes" << endl; return 0; } } } // Sを90度右回転 REP(i, N * 2 - 2) { REP(j, N * 2 - 2) { int match_count = 0; REP(k, i + 1) { REP(l, j + 1) { if ((0 <= (N - 1 - k) && (N - 1 - k) <= N - 1) && (0 <= (N - 1 - l) && (N - 1 - l) <= N - 1) && (0 <= (i - k) && (i - k) <= N - 1) && (0 <= (j - l) && (j - l) <= N - 1)) { if (S90.at(N - 1 - k).at(N - 1 - l) == '#' && T.at(i - k).at(j - l) == '#') { ++match_count; } } } } if (s_count == match_count) { cout << "Yes" << endl; return 0; } } } // Sを180度右回転 REP(i, N * 2 - 2) { REP(j, N * 2 - 2) { int match_count = 0; REP(k, i + 1) { REP(l, j + 1) { if ((0 <= (N - 1 - k) && (N - 1 - k) <= N - 1) && (0 <= (N - 1 - l) && (N - 1 - l) <= N - 1) && (0 <= (i - k) && (i - k) <= N - 1) && (0 <= (j - l) && (j - l) <= N - 1)) { if (S180.at(N - 1 - k).at(N - 1 - l) == '#' && T.at(i - k).at(j - l) == '#') { ++match_count; } } } } if (s_count == match_count) { cout << "Yes" << endl; return 0; } } } // Sを270度右回転 REP(i, N * 2 - 2) { REP(j, N * 2 - 2) { int match_count = 0; REP(k, i + 1) { REP(l, j + 1) { if ((0 <= (N - 1 - k) && (N - 1 - k) <= N - 1) && (0 <= (N - 1 - l) && (N - 1 - l) <= N - 1) && (0 <= (i - k) && (i - k) <= N - 1) && (0 <= (j - l) && (j - l) <= N - 1)) { if (S270.at(N - 1 - k).at(N - 1 - l) == '#' && T.at(i - k).at(j - l) == '#') { ++match_count; } } } } if (s_count == match_count) { cout << "Yes" << endl; return 0; } } } cout << "No" << endl; return 0; }
愚直に並行移動させて一致性を確認しても解けなくはなかったようだが,その場合 # の座標だけのリストを事前に作っておいて探索対象を狭める足切りをしないと解けなかったようだ.
競プロフレンズさんの解説をもとに実装し直したやつ
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; pair<int, int> find_left_top(vector<vector<char>> a, int n) { REP(i, n) { REP(j, n) { if (a.at(i).at(j) == '#') { return make_pair(i, j); } } } return make_pair(-1, -1); } bool judge(vector<vector<char>> s, vector<vector<char>> t, int n) { pair<int, int> s_left_top = find_left_top(s, n); pair<int, int> t_left_top = find_left_top(t, n); int offset_i = t_left_top.first - s_left_top.first; int offset_j = t_left_top.second - s_left_top.second; // cout << offset_i << ":" << offset_j << endl; REP(i, n) { REP(j, n) { int ii = i + offset_i; int jj = j + offset_j; // Tにオフセットをつけてアクセスすることで,並行移動した状態でアクセスできる.賢い. if ((0 <= ii && ii < n) && (0 <= jj && jj < n)) { if (s.at(i).at(j) != t.at(ii).at(jj)) { return false; } } else { // Tの範囲外に#があったら一致する可能性がゼロになるので探索を打ち切る if (s.at(i).at(j) == '#') { return false; } } } } return true; } int main() { cin.tie(0); ios::sync_with_stdio(false); int N; cin >> N; vector<vector<char>> S(N, vector<char>(N)); int s_count = 0; REP(i, N) { REP(j, N) { cin >> S.at(i).at(j); if (S.at(i).at(j) == '#') { ++s_count; } } } vector<vector<char>> T(N, vector<char>(N)); int t_count = 0; REP(i, N) { REP(j, N) { cin >> T.at(i).at(j); if (T.at(i).at(j) == '#') { ++t_count; } } } if (s_count != t_count) { cout << "No" << endl; return 0; } auto rotate = [](vector<vector<char>> a) { long n = a.size(); vector<vector<char>> b(n, vector<char>(n)); REP(i, n) { REP(j, n) { b.at(i).at(j) = a.at(n - 1 - j).at(i); } } return b; }; REP(_, 4) { S = rotate(S); if (judge(S, T, N)) { cout << "Yes" << endl; return 0; } } cout << "No" << endl; return 0; }
ダメだった点
久々だったのでだいぶカンが鈍っている.
良かった点
CV系問題はまだ苦手だが画像の回転と一致性の確認をする方法が学べた.
おわりに
また精進して位置から出直して緑を目指す.
ABC169
過去最高に厳しいABCだった.BとC通せなかったのはそれぞれ1ケースだけWAだったがそのせいでレートを失った.
結果
| 問題 | ACまでに要した時間 | AC | WA | TLE |
|---|---|---|---|---|
| A | 0:45 | 1 | 0 | 0 |
| B | : | 0 | 2 | 0 |
| C | : | 0 | 2 | 0 |
| D | 52:03 | 1 | 0 | 0 |
| E | : | 0 | 0 | 0 |
| F | : | 0 | 0 | 0 |
| 新Rating | Performance | 順位 |
|---|---|---|
| 636 (-4) | 598 | 5786 |
解答
B
1ケースだけWAで死んだ.原因はなにか?
オーバーフロー判定をアホみたいに愚直に書いてそれが動かないケースを踏んだらしい.
だめなやつ
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N; cin >> N; vector<ll> A(N); REP(i, N) { cin >> A.at(i); } sort(A.begin(), A.end(), greater<ll>()); if (A.at(N - 1) == 0) { cout << 0 << endl; return 0; } ll const MAX = 1000000000000000000; ll ans = 1ll; ll prev_ans = ans; REP(i, N) { ans *= A.at(i); if (ans / A.at(i) != prev_ans) { ans = -1; break; } prev_ans = ans; } if (ans > MAX) { cout << -1 << endl; } else { cout << ans << endl; } return 0; }
この実装だと
2 4294967296 4294967296
みたいなケースで4294967296と4294967296の計算をした時点で結果が0になりおかしくなる.これはこの積がちょうどunsigned long longの最大値+1になるためである.
ではこれを回避するにはどうするか.long longの代わりにunsinged long longを使うとこのケースは通せてACになるが,なぜこれがACになるのか良くわかっていない...
ただしくは積を取る前に掛けても大丈夫かを判定する.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N; cin >> N; vector<ll> A(N); REP(i, N) { cin >> A.at(i); } sort(A.begin(), A.end(), greater<ll>()); if (A.at(N - 1) == 0) { cout << 0 << endl; return 0; } ll const MAX = 1000000000000000000; ll ans = 1; REP(i, N) { if (A.at(i) > MAX / ans) { ans = -1; break; } ans *= A.at(i); } if (ans > MAX) { cout << -1 << endl; } else { cout << ans << endl; } return 0; }
C
同じく1ケースだけWAで死んだ.
不動点少数を整数にしたかったのでBを100倍してから積をとったが実はこのタイミングで誤差が出る.
ABC169-Cの犯人一覧です pic.twitter.com/H4zrgf8MuK
— アトム (@atom_HeV) 2020年5月31日
これに気づかなかったのが今回の敗因.
正しくはstringとしてBを受け取り,小数点を取り除いてからstollしてlong longに変換して計算する.こうすれば数学的な結果と一致する.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); ll A; string B; cin >> A >> B; B.erase(1, 1); ll C = stoll(B); cout << A * C / 100 << endl; return 0; }
D
問題文の通り愚直に解いても,素因数分解と素数判定にそれぞれなので計算量的には解ける.もっと効率がいい解き方があるような気がするが今回は愚直に解いた.
B問題,C問題に比べたら「設問に従って解くだけ」なので相当簡易な問題であり,なぜこれがD問題なのか疑問が湧いた.これ200点問題でもよかったのではないか...
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; bool f2(ll v) { if (v <= 2) { return true; } bool ans = true; for (ll i = 2; i * i <= v; ++i) { if (v % i == 0) { ans = false; break; } } return ans; } vector<ll> f(ll v) { vector<ll> ans; for (ll i = 2; i * i <= v; ++i) { if (v % i == 0) { ans.push_back(i); if (i * i != v) ans.push_back(v / i); } } return ans; } int main() { cin.tie(0); ios::sync_with_stdio(false); ll N; cin >> N; vector<ll> y = f(N); y.push_back(N); vector<ll> p; for (ll i : y) { if (f2(i)) { p.push_back(i); } } vector<ll> p2(p); for (ll v : p) { ll v2 = v * v; if (v2 < 0) { continue; } while (v2 < N) { p2.push_back(v2); v2 *= v; if (v2 < 0) { break; } } } sort(p2.begin(), p2.end()); ll ans = 0; ll c = 0; ll idx_mx = p2.size(); while (N > 1 && c < idx_mx) { bool flg = false; for (int i = 0; i < idx_mx; ++i) { if (p2.at(i) == -1) { continue; } if (N % p2.at(i) == 0) { N /= p2.at(i); p2.at(i) = -1; flg = true; break; } } if (!flg) { break; } ++c; ++ans; } cout << ans << endl; return 0; }
ダメだった点
オーバーフロー判定がうまく書けなかった(というかこれはやるべきではなかった)のと計算誤差の配慮が甘すぎた.アルゴリズムと関係ないところで落として本当に情けない結果となった.一応これでもCSで工学修士とった身なのでこれは解けないといけなかった.
良かった点
一応D通して2完にできたのはまぁギリギリ救われた.1完だったら立ち直れなかったかもしれない.
おわりに
- 小数点演算はやらない
- オーバーフロー判定を書かないといけないと思ったらなにかおかしいと考える
ABC166
連続開催ABCの2日目である.しばらくABCはなさそうに見える.
結果
| 問題 | ACまでに要した時間 | AC | WA | TLE |
|---|---|---|---|---|
| A | 0:49 | 1 | 0 | 0 |
| B | 3:40 | 1 | 0 | 0 |
| C | 21:06 | 1 | 0 | 0 |
| D | 54:37 | 1 | 0 | 0 |
| Rating | 順位 |
|---|---|
| 671 (+34) | 3481 |
解答
C
計算量はでいけそうだなと思ったので,双方向グラフとして道を表現して全探索した.
submitでは vector<bool> visitで到達したを記録していたけど,よく考えたらNGじゃない(道がつながっているHよりも高い)
のみをリストアップすれば答えは求められた.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N, M; cin >> N >> M; vector<ll> H(N); REP(i, N) { cin >> H.at(i); } vector<vector<int>> path(N); int a, b; REP(i, M) { cin >> a >> b; --a; --b; path.at(a).push_back(b); path.at(b).push_back(a); } int ans = 0; vector<bool> visit(N, false); REP(i, N) { if (path.at(i).size() == 0 || visit.at(i)) { continue; } visit.at(i) = true; ll h = H.at(i); bool highest = true; for (int const &d : path.at(i)) { if (H.at(d) >= h) { highest = false; break; } } if (highest) { for (int const &d : path.at(i)) { visit.at(d) = true; } ++ans; } } REP(i, N) { if (!visit.at(i)) { ++ans; } } cout << ans << endl; return 0; }
D
の最大値は109なのでビビってしまうが,よく考えれば100を5乗するとその最大値よりも明らかに大きくなる.そのため直感的に探索範囲は大したことがないことが分かる.
また,仮にが109だとすると,
がとり得る最大値はたかだか
である.
よって,なので
の範囲を探索すればいいこと になる.
しかしコンテスト中は,ここまでの考察があまりに短時間でできてしまったために,逆にビビって]の範囲で全探索している.ビビらなければもっと早くACできたはず.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); ll X; cin >> X; vector<ll> A(1100), B(1100); REP(i, 1001) { A.at(i) = B.at(i) = pow(i, 5); } REP(i, 1001) { REP(j, 1001) { if (A.at(i) - B.at(j) == X) { cout << i << " " << j << endl; return 0; } else if ((-1) * A.at(i) - B.at(j) == X) { cout << -i << " " << j << endl; return 0; } else if (A.at(i) + B.at(j) == X) { cout << i << " " << -j << endl; return 0; } } } return 0; }
E(解説AC)
解説読んでAC.
ポイントとしては一致させたい変数を事前計算しておく.
同じに対して
かつ
を満たす組み合わせを数え上げれば解けるが,何も考えずに全探索すると
となりTLE.
そこで,以下のように変形した式の両辺をkey,valueにiまたはjを格納したmapにそれぞれ入れておくと,最終的に両者のkeyが一致するiまたはjの組み合わせを数えればよく, で解ける.
このように分離する利点は,それぞれのmapのkeyがと
にのみ依存し,両者が独立した集合になる点.つまり,それぞれのmapのkeyのみを比較し,valueに含まれているiまたはjの数を乗じるだけで組み合わせ数が分かるため計算がシンプルになる.
これがもしもとの条件のままと
をkeyとすると,valueにはiとjのpairのsetを入れておかねばならず,最後に組み合わせを数え上げる時の判定が面倒くさい.多分これでも解けなくはないが,空間計算量も増加するためメリットは無い.
ここで,はmapへのinsertコストを考慮.最大要素数のvectorを用意してそこに格納していけば
でも解ける気がする.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N; cin >> N; map<ll, set<ll>> L; map<ll, set<ll>> R; ll a; for (ll i = 1; i <= N; ++i) { cin >> a; ll l = i + a; ll r = i - a; if (L.find(l) == L.end()) { set<ll> s; s.insert(i); L.insert(make_pair(l, s)); } else { L.at(l).insert(i); } if (r > 0) { if (R.find(r) == R.end()) { set<ll> s; s.insert(i); R.insert(make_pair(r, s)); } else { R.at(r).insert(i); } } } ll ans = 0; for (auto const &it : L) { if (R.find(it.first) != R.end()) { ans += it.second.size() * R.at(it.first).size(); } } cout << ans << endl; return 0; }
ダメだった点
Dに時間をかけすぎた.根拠のありそうな解析が済んだらさっさとsubmitした方が結果的に良かっただろうと思う.早い緑コーダーは30分程度でsubmitしていたのでそれぐらいで解けるべきであった.
良かった点
難易度が低めなABCだったと思うがそれでもとりあえずABCDの4完を達成できたのは良かった.Eも解ければもっと良かったが以外の解法が思いつかなかった.
おわりに
- 3ヶ月ぶりに最大レートを更新できた.
- 緑まであと129となり,平均+30のレートアップを5回達成すれば緑になれる.
- こう書くとまだ道のりが長い気がするが,解ける問題を増やして一気にレートを100ぐらいポンと上げて緑入りするシナリオを狙いたい.
- AtCoder ProblemsのBoot campを解いているのがいい感じに効いている.やはり数をこなさなければ自分のレベルだとABCで上に行けないことがよく分かる.
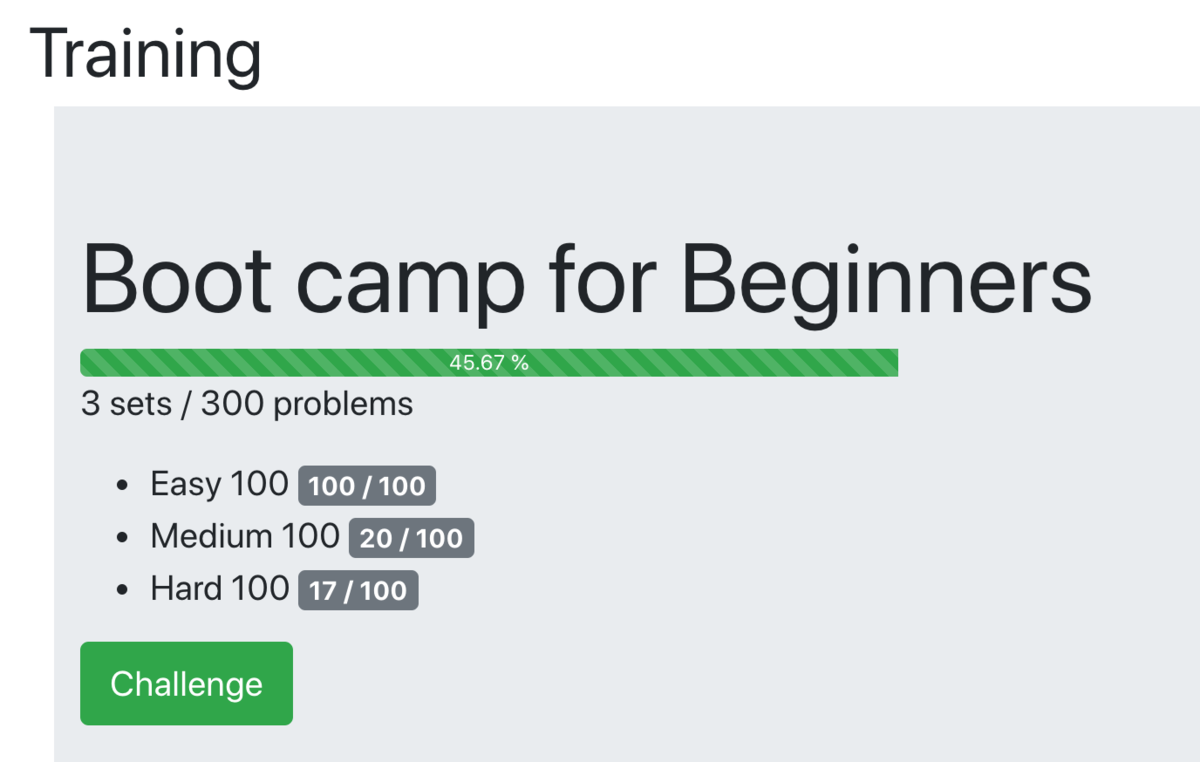
ABC165
2日連続開催ABCの1日目.
結果
| 問題 | ACまでに要した時間 | AC | WA | TLE |
|---|---|---|---|---|
| A | 1:41 | 1 | 0 | 0 |
| B | 27:58 | 1 | 0 | 0 |
| C | : | 0 | 0 | 0 |
| D | 59:35 | 1 | 0 | 1 |
| Rating | 順位 |
|---|---|
| 637 (+28) | 4141 |
解答
C(解説AC)
解けなかった.
考えていたこと
- すべての式を連立方程式とみなしても答えは一意に決まる訳じゃなさそうだしどうするか.
- 仮にそうだとしてもどう表現してどう実装すればいいか分からん.
- 仮に全列挙する場合,無条件で並べれば1010だし全探索は間に合いそうにない(これは勘違い.広義単調増加数列なので最大の空間計算量は
).
- わからん.ダメだ.次いこ.
すぬけさんの解説放送観ながら解いたやつ.vector<T>.back() をうまく使うと最小桁以上の値のみを次にpushできるため結果的に広義単調増加数列になる.頭良すぎてワラタ.これを応用すると(広義)単調減少数列も作れる.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; vector<int> a, b, c, d; int N, M, Q; int ans; void dfs(vector<int> A, int size) { if (size == N) { int now = 0; REP(i, Q) { if (A.at(b.at(i)) - A.at(a.at(i)) == c.at(i)) { now += d.at(i); } } ans = max(ans, now); return; } A.push_back(A.back()); while (A.back() <= M) { dfs(A, size + 1); ++A.back(); } } int main() { cin.tie(0); ios::sync_with_stdio(false); cin >> N >> M >> Q; a = b = c = d = vector<int>(Q); REP(i, Q) { cin >> a.at(i) >> b.at(i) >> c.at(i) >> d.at(i); --a.at(i); --b.at(i); } ans = 0; dfs(vector<int>(1, 1), 1); cout << ans << endl; return 0; }
D
解析的に解けなさそうと思い,適当にxを大きくして数式の結果をprintしたら周期性が見えたのと,何となく数式からも周期性が垣間見えるのでそれで出したらAC
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); long double A, B, N; cin >> A >> B >> N; long double a_b = A / B; long double x = min(N, B - 1); cout << floor(a_b * x) - A * floor(x / B) << endl; return 0; }
考えていたこと
- もうダメだ
- とりあえずどういう動きするか分からないので
をxごとにprintしてxに対してどう反応するか見てみるか
- お,周期性あるやん.しかも最大値は一定
- 言われてみれば
は単調増加していくけど
はxの値に関係なくB-1以上にはならないので周期性が生じるのも分かる気がする.
- じゃあ
で与題は最大になるのか?
- やってみるか.通った.マジか.
E(解説AC)
コンテスト中は全く解法が思いつかなかった問題.しかし適当にNとMを設定してみるとどういう時にダメになるかは明確.
イメージとしては,以下のように問題を噛み砕くと解法が分かる.
- N人のメンバーを
]の数列の上に並べ,その数列上で各メンバーを右に一個ずつスライドさせる操作をN回行う.その間に,対戦卓に書かれた番号(
とする)と,その時点でメンバーがいる数値と一致した時に同じ相手と2回以上当たったらNG.
- 対戦卓に入ったときに同じやつと2回以上当たる条件は,対戦卓の番号の差が同じ時.∵各メンバーの数値は固定で1だけ単調増加するため差は変化しない.
- 一方で,N+1の番号になったメンバーは1に戻るため,Nが偶数の場合は
と
が一致する場合も上記の理由で2回当たってしまうためNGとなる.奇数の場合はこのケースは発生しない*1.
- 以上の考察により,
]において左端(1)と右端(N)から順番に舐めていき,
かつ一度も見たことがないパターンを列挙していけばよい.そのようなパターンに遭遇したら左端か右端をどちらか一個進めることで回避できる.
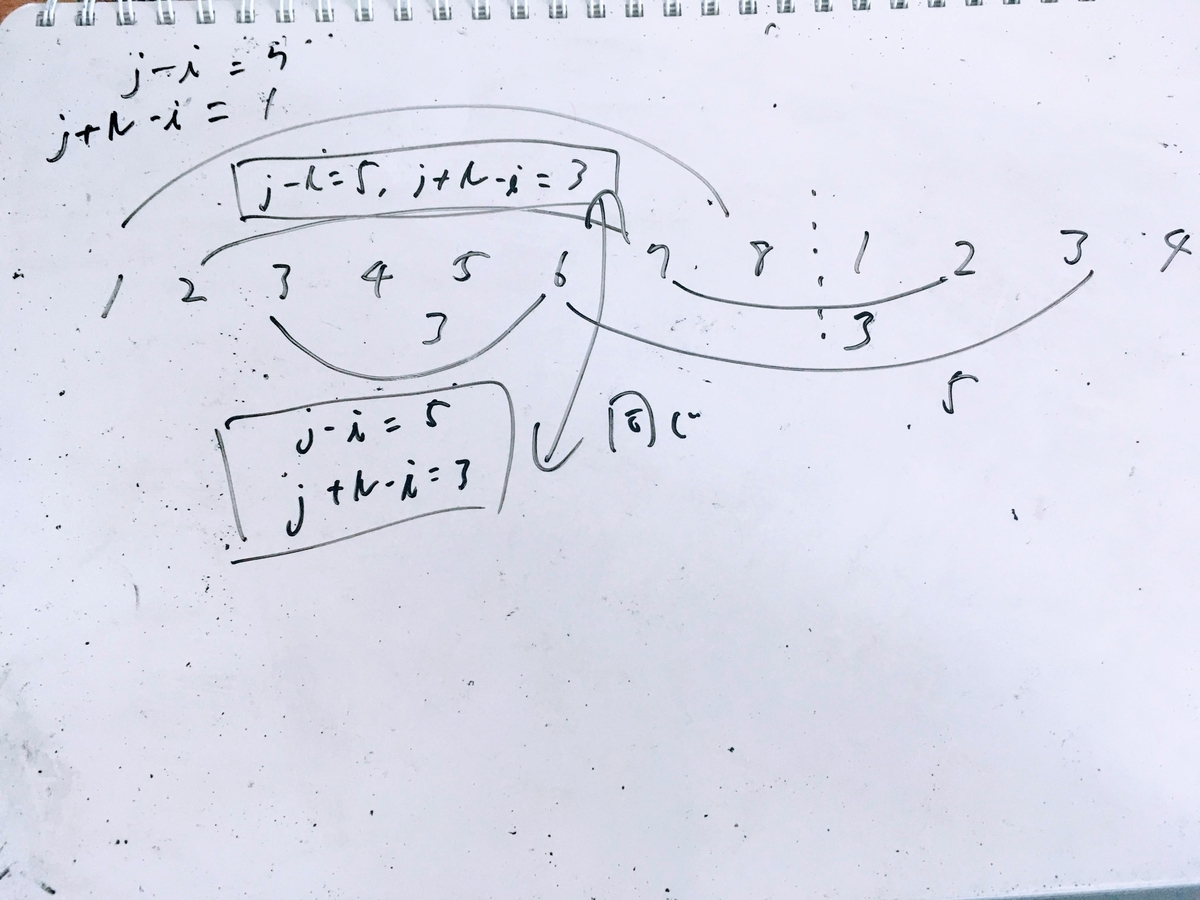
と
の関係
自分の考察は上記のリストのうち2番目にすら至らなかった.できなかった理由として,他の解答者がやっているような「最小のNとMのケースで考える」を試さなかった為であると考えられる.
似たようなパターンで「直線上に並んだN個の家の任意の家から別の任意の家へ移動するときの最短距離を求めよ」みたいな問題を見たことがある.これはで解けたが,循環数列(と見なせるもの)に対する操作を可能にする条件を求める問題も典型問題のうちのようだ.今後は解けるようになっておく必要がある.でもこの問題は青パフォ問題みたいだしやっぱ難しい部類だったとは思う.
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N, M; cin >> N >> M; int l = 1; int r = N; if (N % 2 == 1) { REP(i, M) { cout << l << " " << r << endl; ++l; --r; } } else { set<pair<int, int>> found; REP(i, M) { cout << l << " " << r << endl; ++l; --r; if (abs(r - l) == abs(l + N - r) || found.find(make_pair(min(abs(r - l), abs(l + N - r)), max(abs(r - l), abs(l + N - r)))) != found.end()) { ++l; } found.insert(make_pair(min(abs(r - l), abs(l + N - r)), max(abs(r - l), abs(l + N - r)))); } } return 0; }
追記
ABC165の解説放送を観るとすぬけさんがとても分かりやすい解説をしていた.
多角形としてN人のメンバーを並べると,対戦卓の組合わせをそれぞれの角をつなぐ線分として表現できる.この図を使うとどういうケースでOKになるか直感的に理解できる.

ここから学べる点としては,今回のような循環する数列を扱う場合には図で考えるのも一つの手段である.
ダメだった点
- Cの計算量を正確に見積もれなかった.単調増加数列なんだから全パターン拾っても
で済むというのは思いついてくれ.
- Bで一瞬怯んでしまったので飛ばして後でやろうとしたら他も難しかった->結果的にBのsubmitが遅くなって結果に影響したというパターンをまたやってしまったのでよくない.Bは瞬殺できるものとして絶対後回しにしない.
- Dはたまたま解けたけどあんまり再現性ないな.floor関数は
のようにモジュロ演算に置き換えて整数の世界だけで計算できることがわかったので,次回以降は解析的に解きたい.
- あとモジュロ演算の特性ももう一度計算しておく必要がある.Dはモジュロ演算の分配則を知らないと解析的には解けない.
良かった点
- Cが解けず,DのACも遅かったのでレートが下がるんじゃないかとヒヤヒヤしたがプラスになって良かった.B速解きができればもう少しレート挙げられただろうが.
おわりに
- パフォーマンスの分布を見ると,800以下のレートだとABC速解きが依然として高パフォーマンスを得る効果的な方法のように見える.
- しかし,今後緑,水色と上がっていった時にそれでは通用しなくなるのは傾向から明らかなので解けない問題をへらす努力も継続して必要.
- 全探索が実装できなかった点は大いに反省し,単調増加,単調減少,条件なしの3パターン数列の全列挙はできるようになっておく必要がある.
*1:色んな人の解説を読んだがこれを明確に説明しているものはなかった.謎
ABC162
しばらく間が空いてしまったが再開する.大学院卒業して仕事に復帰したら競プロどころじゃなくなってしまっていた.これから本気だす.
今回はC問題でやらかしてめちゃくちゃ順位落とした..情けない.
今日の反省点として,ABC162C問題でコンパイルオプションに`-O2`つけ忘れてローカルでTLEしてるケースを必死に最適化して30分浪費した.即出してれば順位が1000は上がった.ちゃんとレギュレーションは読まなければならぬ.
— Kazuhiro Serizawa (@seri_k) 2020年4月12日
結果
| 問題 | ACまでに要した時間 | AC | WA | TLE |
|---|---|---|---|---|
| A | 2:22 | 1 | 0 | 0 |
| B | 4:18 | 1 | 0 | 0 |
| C | 62:07 | 1 | 0 | 0 |
| D | : | 0 | 0 | 1 |
| Rating | 順位 |
|---|---|
| 538 (-26) | 7427 |
解答
A
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N; cin >> N; while (N > 0) { int n = N % 10; if (n == 7) { cout << "Yes" << endl; return 0; } N /= 10; } cout << "No" << endl; return 0; }
B
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N; cin >> N; ll ans = 0; REPI(i, 1, N + 1) { if (i % 3 == 0 || i % 5 == 0) { continue; } ans += i; } cout << ans << endl; return 0; }
C
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int K; cin >> K; if (K == 1) { cout << 1 << endl; return 0; } map<pair<int, int>, int> memo; ll ans = 0; REPI(i, 1, K + 1) { REPI(j, 1, K + 1) { memo.insert(make_pair(make_pair(i, j), __gcd(i, j))); } } for (auto it : memo) { REPI(k, 1, K + 1) { ans += memo.at(make_pair(it.second, k)); } } cout << ans << endl; return 0; }
D
TLE
#include <bits/stdc++.h> #define REP(i, x) REPI(i, 0, x) #define REPI(i, a, b) for (int i = int(a); i < int(b); ++i) #define ALL(x) (x).begin(), (x).end() typedef long long ll; using namespace std; int main() { cin.tie(0); ios::sync_with_stdio(false); int N; string S; cin >> N >> S; map<pair<int, int>, int> C; REP(i, N) { char i_c = S.at(i); for (int j = i + 1; j < N - 1; ++j) { if (S.at(j) != i_c) { C.insert(make_pair(make_pair(i, j), j - i)); } } } ll ans = 0; for (auto it : C) { pair<int, int> i_j = it.first; // cout << i_j.first << ":" << i_j.second << ":" << it.second << endl; for (int k = i_j.second + 1; k < N; ++k) { if (k - i_j.second == it.second) { continue; } if (S.at(k) != S.at(i_j.first) && S.at(k) != S.at(i_j.second)) { ++ans; } } } cout << ans << endl; return 0; }
ダメだった点
レギュレーションでgcc C++は -O2 オプション指定なのにローカルでつけておらず,C問題のK=200のケースが3秒以上かかっていて必死に最適化していて時間を浪費してしまった.
レギュレーションに従い,今後は常に g++ -std=gnu++17 -Wall -Wextra -O2 でコンパイルする.
なお普段はaliasを張って使っている.
alias cp14="clang++ -std=c++14 -Wall -Wextra -O2" alias cp11="clang++ -std=c++11 -Wall -Wextra -O2" alias gp14="g++-9 -std=c++14 -Wall -Wextra -O2" alias gp17="g++-9 -std=c++17 -Wall -Wextra -O2"
良かった点
gcdのメモ化を思いついたのは偉いが結局 でも間に合ったので早すぎる最適化に過ぎなかった.
おわりに
前回-63,今回-26とレーティングを落としまくっていてかなり凹んでいる.しかしようやく仕事のペースにも慣れてきたので挽回していきたい.